Konig定理和匈牙利算法(其实是增广路算法)
Konig定理
点覆盖:节点的集合,满足每条边至少有一个端点被选
最小点覆盖: 点数最少的点覆盖
Konig定理: 在一个二分图中,最大匹配数等于最小点覆盖
证明:
首先,因为匹配边没有共同的端点,而一个点覆盖中每条边至少有一个端点被选,所以所有点覆盖大于等于最大匹配
接下来我们只要能构造出一个等于最大匹配数的点覆盖就可以证明Konig定理
在最大匹配中,一条边有四种情况:
- 匹配边
- 非匹配边,两端点都参与匹配
- 非匹配边,只有左端点参与匹配
- 非匹配边,只有右端点参与匹配
接下来我们这么构造点覆盖:
- 对于只有左端参与匹配的非匹配边,选取它的左端点
- 把端点被选中的边去掉,重复步骤1
- 对于剩下的匹配边选它们的右端点
首先,选的点都是匹配边的端点,所以选出来了最大匹配数个点,也是因为这个,所有匹配边肯定被覆盖。接下来考虑所有非匹配边,重复过步骤1之后,所有第三种边都被覆盖;在最后一步之后,就能把第二种和第四种覆盖。于是所有边都被覆盖了,选出来的点确实组成点覆盖。
Q.E.D
匈牙利算法 (其实是增广路算法)
交错路(alternating path):由匹配边与非匹配边交错而成 (只有一条边也可以)
增广路(augmenting path): 起点和终点都不参与匹配的交错路
枚举起点,不停找增广路
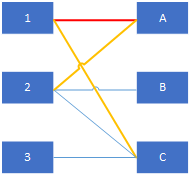
找到之后反转一下(匹配边变非匹配边,反之亦然)就能使匹配数增加一
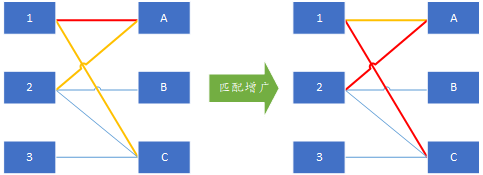
没有增广路之后就得到了最大匹配
注意到这个过程中原先的匹配点不会变成非匹配点,只可能会新增匹配点
枚举起点时,每个非匹配点只需要被枚举一次,如果以它为起点存在增广路,那增广后它就不能再作为起点,因为它变成匹配点了,而如果不存在增广路,也就是找不到终点是非匹配点的交错路,那之后也不可能再找到增广路,因为不会新增非匹配点。
在此基础上,我们只需要枚举左侧点,假设左侧点都被增广过之后,右侧点还有未匹配的,那么以它们为起点不可能有增广路,因为以它们为起点的增广路的终点一定在左侧点中(因为增广路长度肯定是奇数)但是这与所有左侧点已经被增广过矛盾(增广的时候就应该找到这条增广路了)
综上,我们只需要枚举每个左侧点1次
代码
//假设左边的点编号为[1,nL]
bool vst[NV]; //表示右侧的点在这轮寻找增广路的时候有没有被访问过
int match[NV]; //表示右侧的点匹配上了左侧的哪个点
//返回值代表有没有找到增广路
bool find(int u) {
for (int i = hd[u]; i; i = e[i].nxt) {
int v = e[i].to;
if (vst[v]) continue;
vst[v] = true;
if (!match[v] || find(match[v])) {
match[v] = u;
return true;
}
}
return false;
}
int Hungarian() {
int maxMatch = 0;
for (int u = 1; u <= nL; u++) {
memset(vst, 0, sizeof(vst));
maxMatch += find(u);
}
return maxMatch;
}
Berge's theorem
一个匹配是最大匹配当且仅当这个二分图中不存在增广路。这个定理保证了上述算法的正确性。
正方向是很显然的,接下来证明反方向。
条件是当前的匹配M下二分图不存在增广路。使用反证法,假设匹配M'比匹配M更大(M'和M是匹配边的集合)
令D为M与M'的对称差,那么D中的边要么能组成长度为偶数的回路,要么就是在M与M'间交替的路径,因为D中每个节点最多能连接两条边(一条M的,一条M'的),而形成回路的路径中在M中的边的数量与在M'中的边的数量是相等的,于是回路一定是偶数长度的。
因为M'比M更大,所以D中一定存在某个极大的分量其中在M'中的边的数量比在M中的边的数量多,这样的一条路径一定是以M'中的边开始,M'中的边结束的极大的路径,注意到这个路径中在M'中的边是不在M中的(对称差定义),而且对于它的起点和终点,它们在M中一定是未匹配点,否则要么路径不是极大的,要么M'就是个不合法的匹配。
综上,这就意味着存在一条增广路,但是这与条件不存在增广路矛盾。
Q.E.D