注：本文只考虑整数容量、整数流，但一部分论证可以直接推广到非整数流的问题上

什么是网络流

首先，网络（flow network）是指一个有向图 $G=(V,E)$，其中有两个特殊点: 源点（source）$s \in V$ 和汇点（sink）$t \in V$（$s \neq t$）

容量网络（capacity network）：加了容量的网络，上面每条边的权值等于这条边的容量

容量 $c$ 是一个 $V\times V\rightarrow R$ 的映射, 规定：

如果 $(u,v)\in E$ 那么 $c(u,v)>0$

否则 $c(u,v)=0$

容量网络

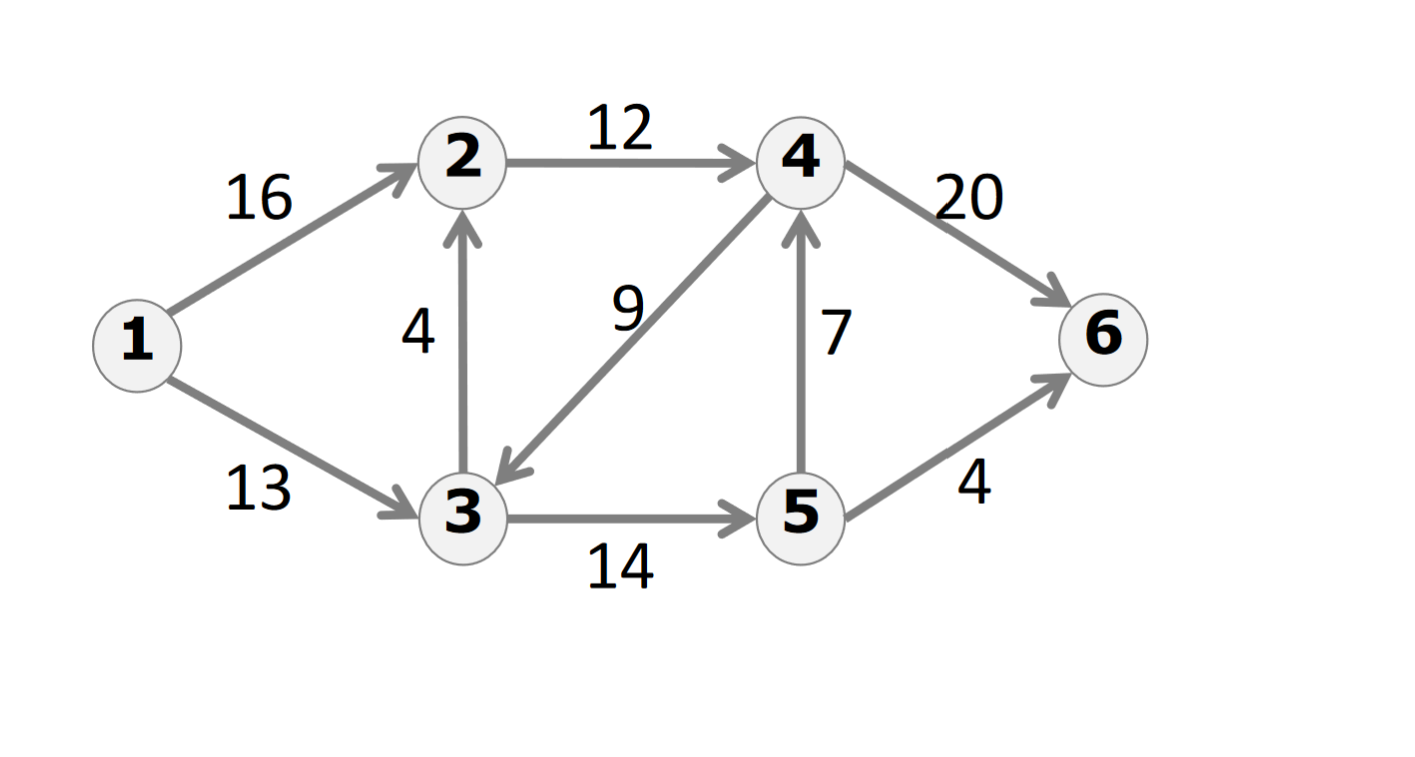
流量网络（flow network）：加了流量的网络，x/y表示流量/容量

流量网络

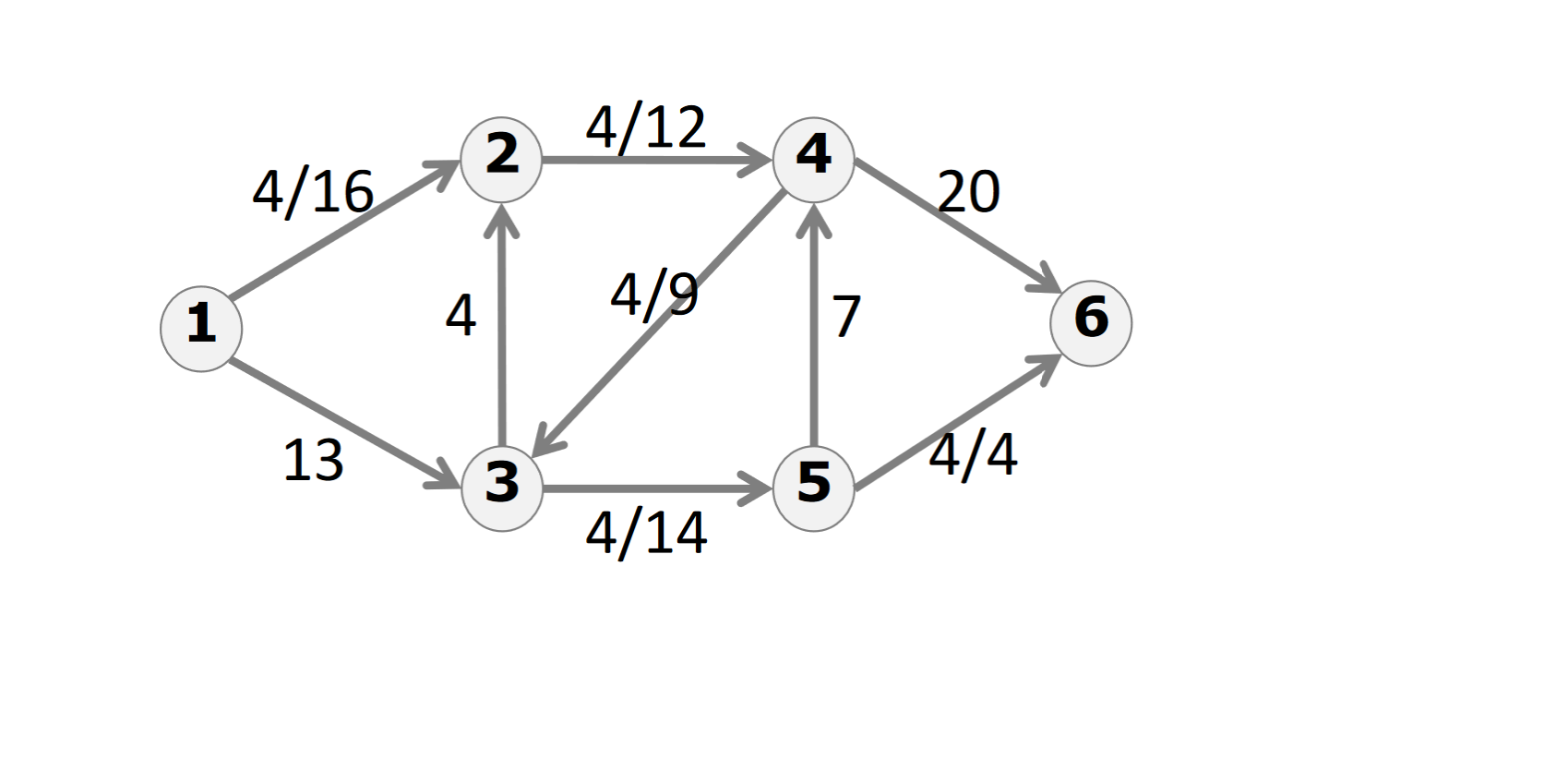
流量 $f$ 也是$V\times V\rightarrow R$的映射

它要满足如下三个性质：

  1. 容量限制：$f(u,v) \le c(u,v)$
  2. 斜对称性（skew symmetry）：$f(u,v)=-f(v,u)$
  3. 流守恒性：流入一个点的流量等于流出这个点的流量 $\forall u \in V-\{s,t\},\sum\limits_{v \in V}{f(u,v)}=0$

注意到由1和2:

  1. $(u,v) \notin E \wedge(v,u) \notin E \implies f(u,v)=f(v,u)=0$
  2. $f(u,u)=0$

流的大小定义为 $v(f)=\sum\limits_{v\in V}{f(s,v)}$

为了便于讨论，定义符号$F(S,T)=\sum\limits_{u\in S}\sum\limits_{v\in T}f(u,v)$

那么显然有:

  1. $F(S,T)=-F(T,S)$
  2. $F(A\cup B,C)=F(A,C)+F(B,C)-F(A\cap B,C)$ 第二个参数也是同理
  3. $s\notin S\wedge t\notin S\implies F(S,V)=F(V,S)=0$

由此可以推出 $|f|=F(s,V)=F(V,V)-F(V-s,V)=-F(V-s,V)=F(V,V-s)=F(V,V-s-t)+F(V,t)=F(V,t)$

残量网络（residual network）：$G$中所有结点和剩余容量大于 $0$ 的边和反向边构成的图，一般记作 $G_f$

形式化地，$G_f=(V,E_f)$，其中 $E_f=\{(u,v)|c_f(u,v)>0,u\in V,v\in V\}$，其中 $ c_f(u,v)=c(u,v)-f(u,v) $ 即剩余流量（residual capacity）

残量网络

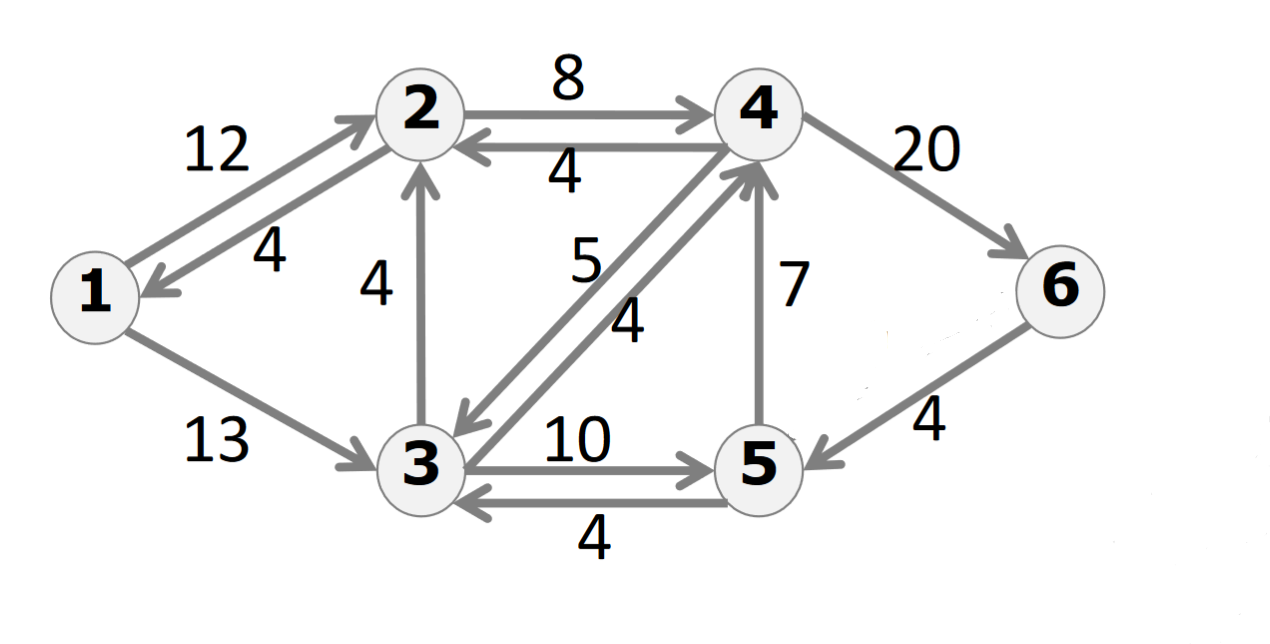
最大流

最大流就是大小最大的流

增广路径就是残量网络上从源点到汇点的一条路径

增广路径

不停地找增广路径（然后在残量图上修改相应的流量）直到没有任何增广路径，我们就可以得到最大流 - 这就是增广路定理（之后会论证这个定理）

实际上流的斜对称性就是用来“退流”的，比如我们之前选的流不够好，它就能撤销掉之前的流

算法

Ford-Fulkerson: 每次通过dfs找一条增广路径

复杂度: $\mathcal{O}(|E||f|)$ 其中$f$是最大流

是最简单的最大流算法，但是复杂度很差，在有些图上运行时间会和容量成正比

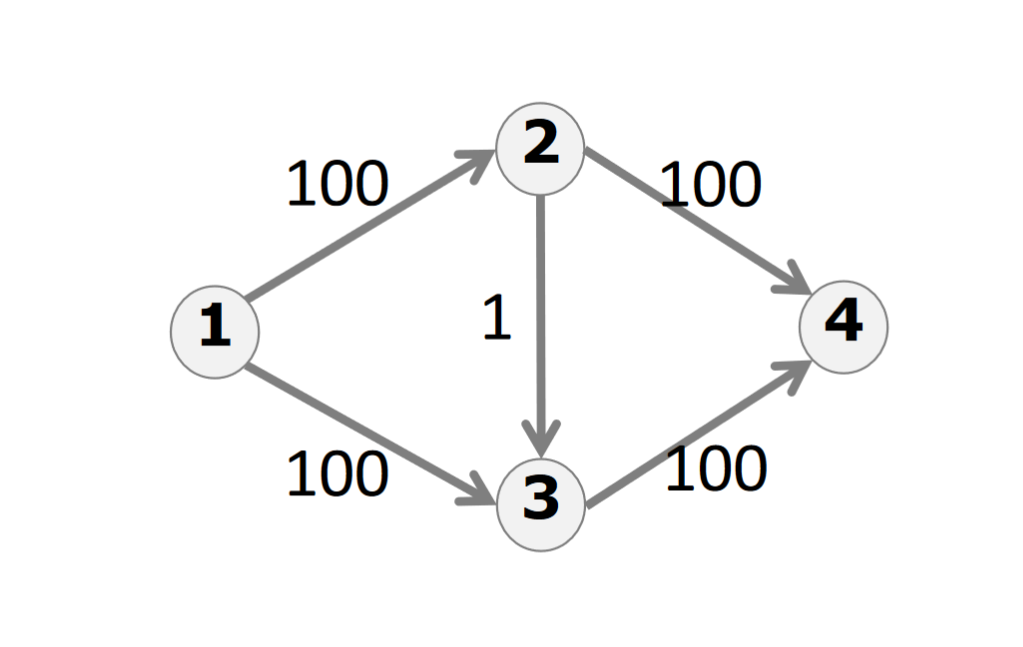
Ford-Fulkerson Killer（如果每次dfs运气不好都过中间那条边的话，算法就要找200次增广路了） Ford-Fulkerson Killer

Edmond-Karp动能算法: 每次通过bfs找一条增广路径

找到的增广路径叫做最短步数增广路(SAP, Shortest Augmenting Path)

复杂度：$\mathcal{O}(|V||E|^2)$ 证明

实际效果: 1秒可以处理上万个节点的稀疏图，通常运行速度达不到这个上界这么慢

代码
int pre[NV], flow[NV];

bool bfs() {
    queue<int> q;
    memset(pre, 0, sizeof(pre));
    pre[S] = -1;
    flow[S] = INF;
    q.push(S);
    while (!q.empty()) {
        int u = q.front(); q.pop();
        for (int i = hd[u]; i; i = e[i].nxt) {
            int c = e[i].c;
            if (!c) continue;
            int v = e[i].to;
            if (pre[v]) continue;
            q.push(v);
            pre[v] = i;
            flow[v] = min(flow[u],c);
            if (v == T) return true;
        }
    }
    return false;
}

int EK() {
    int maxFlow = 0;
    while (bfs()) {
        maxFlow += flow[T];
        for(int u = T; u; u = e[pre[u]^1].to){
            e[pre[u]].c -= flow[T];
            e[pre[u]^1].c += flow[T];
        }
    }
    return maxFlow;
}

Dinic: bfs+dfs每次尝试寻找多条增广路径

复杂度：$\mathcal{O}(|V|^2|E|)$ 证明

实际效果: 1秒可以处理上万个节点的稀疏图，复杂度往往达不到这个上界，所以不能通过将$|V|$,$|E|$代入$|V|^2|E|$来估计算法复杂度

使用bfs分层+dfs多路探索以及当前弧加速（current-arc acceleration）

注意：当前弧加速是必须要有的，它是用于保证时间复杂度正确性的一部分，而多路探索是常数优化

设$d(u)$为从源点bfs到u的轮数+1，然后根据$d(u)$对残量图进行分层得到层次图

形式化地，定义$G_L=(V,E_L)$为$G_f$的层次图，$E_L=\{(u,v)|(u,v)\in E_f, d(v)=d(u)+1\}$

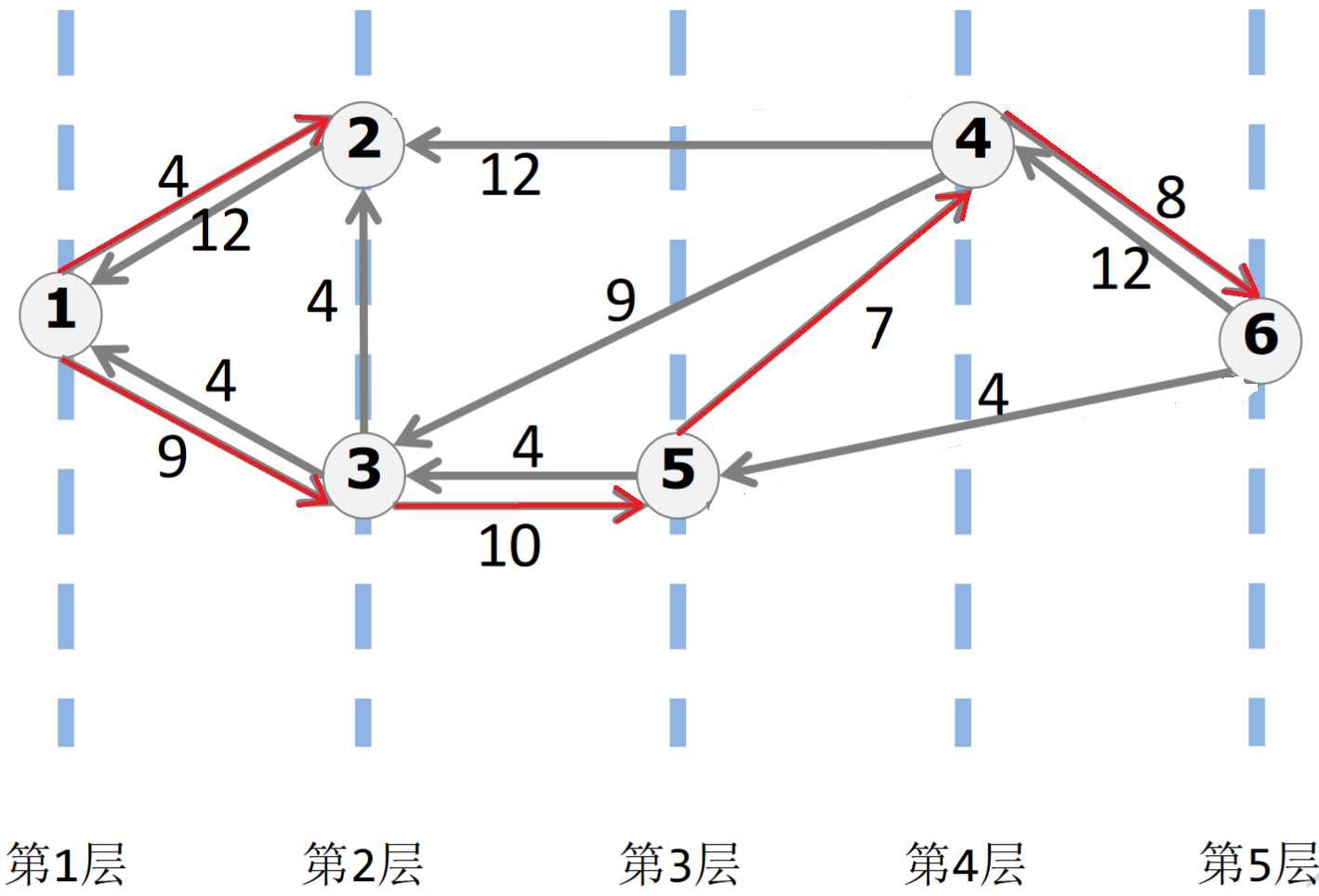层次图 (黑边残量图，红边层次图)

每轮bfs求出$G_L$后在它上面dfs多路探索得到它上最大的流，然后修改残量图并给答案加上这个流

dfs多路探索的时候我们要应用当前弧加速，当前弧加速就是说，因为我们可以提前知道哪些路径走下去肯定到不了终点，我们就可以提前决定不去走它们

int S, T;
int lv[N];
int cur[N]; //这个就是当前弧加速

bool bfs() {
    memset(lv, 0, sizeof(lv));
    queue<int> q;
    q.push(S);
    lv[S] = 1;
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = hd[u]; i; i = e[i].nxt) {
            int c = e[i].c;
            if (!c) continue;
            int v = e[i].to;
            if (lv[v]) continue;
            q.push(v);
            lv[v] = lv[u] + 1;
        }
    }
    return lv[T];
}

int dfs(int u, int f) {
    if (u == T) return f;
    int sum = 0;
    for (int i = cur[u]; i && f; i = e[i].nxt) {
        cur[u] = i; //这条边所有的流量已经被用掉了，后面再来这个结点的时候不需要再走这条边了
        int v = e[i].to;
        int c = e[i].c;
        if (lv[v] != lv[u] + 1 || !c) continue; //这条边其实不在层次图里面
        int delta = dfs(v, min(f, c)); //这是多路探索，就是不需要每次都从源点开始找增广路径
        sum += delta;
        f -= delta;
        e[i].c -= delta;
        e[i ^ 1].c += delta;
    }
    return sum;
}

int Dinic() {
    int maxFlow = 0;
    while (bfs()) {
        for (int i = 1; i <= n; i++) cur[i] = hd[i]; //每次dfs前要重置这个
        maxFlow += dfs(S, INF);
    }
    return maxFlow;
}

最小割

一个割$(S,T)$就是满足$s\in S\wedge t\in T$的对$V$的划分

割的大小定义为 $v(S,T)=\sum\limits_{u\in S}\sum\limits_{v\in T}c(u,v)$，最小割定义为大小最小的割

最小割另一个等价的定义是最小的通过删边使源点到汇点不再连通的删去的边的权值和（等价是因为最小割肯定是分为$s$可达点和$s$不可达点的割）

引理：对于任意的割$(S,T)$和流$f$，$|f|=F(S,T)$

证明：$|f|=F(s,V)=F(s,V)+F(S-s,V)=F(S,V)=F(S,T)+F(S,S)=F(S,T)$

最大流最小割定理

即最大流等于最小割

证明：由上面的引理容易得到对任意的流和割，$|f|\le v(S,T)$

那么如果存在一个流和一个割满足 $|f| = v(S,T)$ 就可以证明该定理（若这个 $f$ 不是最大流，显然会产生矛盾）

假设我们根据之前的 Ford-Fulkerson 算法找到了一个流（当然还不知道是最大流），那残量网络中肯定没有从$s$到$t$的路径（算法终止条件），于是我们可以把点划分为$s$可达的$S$和$s$不可达的$T$，得到一个割 $(S,T)$。

对于所有满足$u\in S,v\in T$的点对$(u,v)$，由于残量图中$s$可以达到$u$，但不能达到$v$，所以$c_f(u,v)\le0\implies f(u,v)\ge c(u,v)$，然而$f(u,v)\le c(u,v)$，所以$f(u,v)=c(u,v)$

由引理可得，$|f|=v(S,T)$

Q.E.D

应用

1. 二分图最大匹配

比如对于这个二分图

二分图

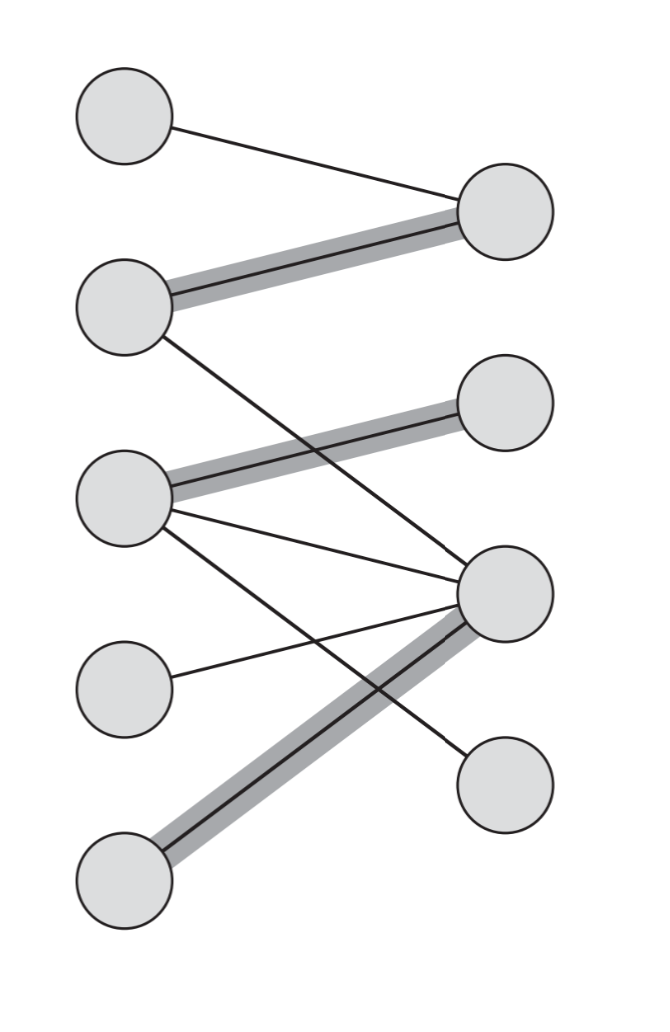
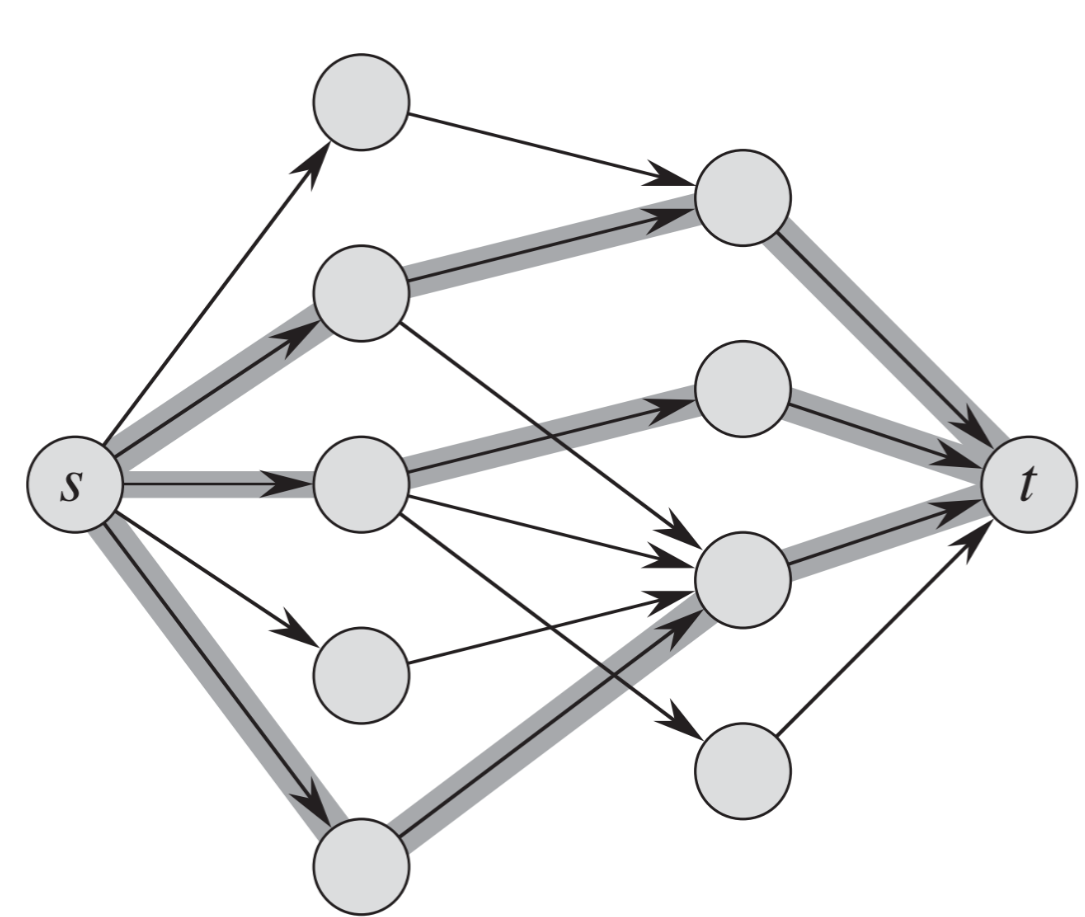
这么建图，然后再上面跑一遍最大流就可以得到最大匹配了（下图中每条边的边权都是1，反向边省略）

二分图最大匹配

2. 对“二选一”类型的问题建模

比如有$n$个物品要放入集合$A$或集合$B$，第$i$个不放$A$要消耗$u_i$，不放$B$要消耗$v_i$，$i$和$j$不在一起要消耗$w_{ij}$，求最小消耗

那我们可以先建立一个超级源和超级汇，超级源到$i$的边权为$u_i$，$i$到超级汇的边权为$v_i$，$i$和$j$连权值为$w_{ij}$的双向边，在这张图上跑最小割，就可以得到最小消耗

可以用$+\infty$表示$i$和$j$必须放在一起

例题

第一题

幼儿园里有n个小朋友打算通过投票来决定睡不睡午觉。

对他们来说，这个问题并不是很重要，于是他们决定发扬谦让精神。

虽然每个人都有自己的主见，但是为了照顾一下自己朋友的想法，他们也可以投和自己本来意愿相反的票。

我们定义一次投票的冲突数为好朋友之间发生冲突的总数加上和所有和自己本来意愿发生冲突的人数。

我们的问题就是，每位小朋友应该怎样投票，才能使冲突数最小？

解法

这个问题很符合上面“二选一”的模型

我们可以从超级源向每个要睡觉的小朋友连一条权值为1的边，从超级汇向每个不要睡觉的小朋友连一条权值为1的边，好朋友之间连一条权值为1的双向边，再跑最小割就能得到答案了。

第二题

在一个n*n的方格里，每个格子里都有一个正整数。

从中取出若干数，使得任意两个取出的数所在格子没有公共边，且取出的数的总和尽量大。

输入：

第一行是n，接下来n行是n*n方阵

解法

因为最大总和等于所有数的和减掉最小的不选的总和

所以我们考虑如何用最小割建模最小的不选的总和

首先把格子按行号与列号的和的奇偶性分类

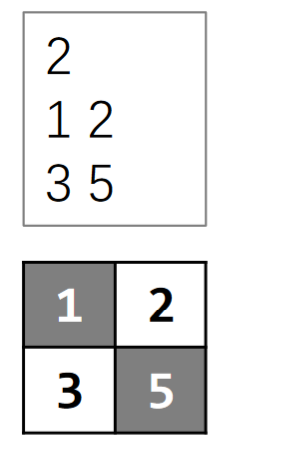
从源点向偶格子连边，权值为格子中的值；从奇格子向汇点连边，权值为格子中的值；从偶格子向它周围的四个奇格子连边，权值为$+\infty$

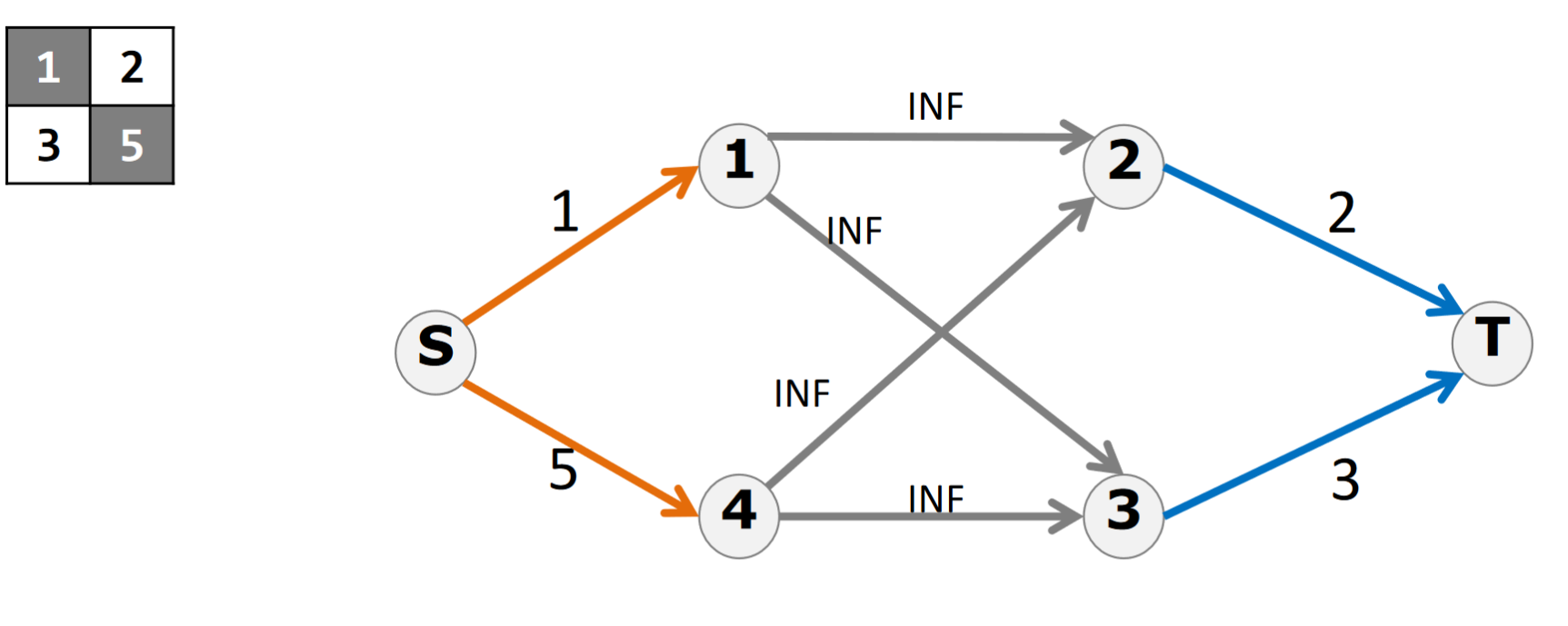
按照集合划分理解

考虑一个割$(S,T)$

对于一个奇格子，在$S$里是选它，在$T$里是不选它；对于偶格子，在$S$里是不选，在$T$里是选。

如果一个奇格子是$S$，它连着的偶格子都是$S$，就代表不选偶格子（偶格子不能是$T$，因为奇格子都偶格子连了个无限大的边，如果是$T$那这个割就不可能是最小割了）

奇格子是$T$，偶格子也是$T$，就代表不选奇格子

奇格子是$T$，偶格子是$S$，就代表都不选

求出最小割，就是最小的不选的总和了

按照割边来理解

首先无限大的边肯定不能割，而如果我割左边一条边（图中橙边），那么就表示我不要奇格子，然后右边连接着的偶格子就有保留的机会了

而如果我不割左边割右边（图中蓝边），那么我就必须把相应的4个（或2个3个）全部割掉才能使图不连通，如果我这时候突然又决定把左边割掉，那么其实是不划算的（割左边的话就没必要割右边了，因为我们要最小割，而割左边是前面一个情况）

由此可见这是保证了不能选相邻格子的限制的