第一题

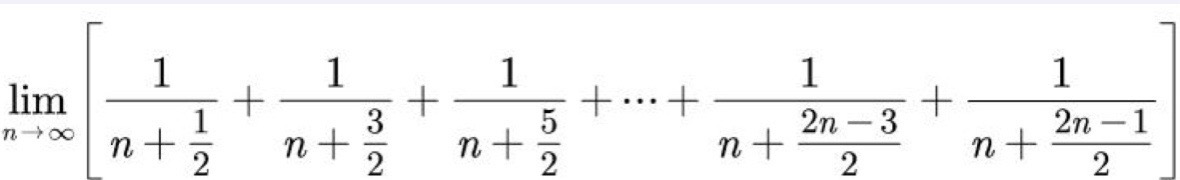
相当于在近似$y=\frac{1}{x}$在$n$到$2n$的曲线下方面积, 所以结果是 $\ln{2n}-\ln{n}=\ln{2}$

第二题

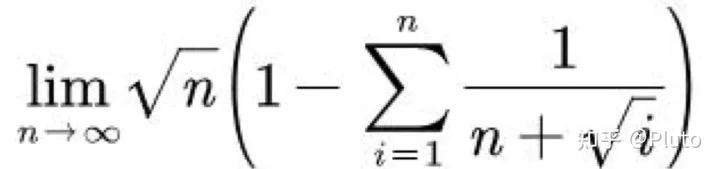
$ \begin{aligned} 原式&=\lim_{n \to \infty}{\sqrt{n}(\sum_{i=1}^{n}{\frac{\sqrt{i}}{n^2+n\sqrt{i}}})} && \text{}1{拆成}n{个}\frac{1}{n}{各自相减得到}\\ &=\lim_{n \to \infty}{\sqrt{n}(\sum_{i=1}^{n}{\frac{i^{\frac{1}{2}}}{n^2}})} && \text{}n{趋于无穷，}n^2{增长快过}n\sqrt{i}\\ &=\lim_{n \to \infty}{n^{\frac{1}{2}}{\frac{\frac{2}{3}n^{\frac{3}{2}}}{n^2}}} && \text{}n{趋于无穷，求和相当于积分}\\ &=\frac{2}{3} \end{aligned} $